在几何问题的考查中,会遇到求解最短距离的题目,其中最短距离指的是:两点之间线段最短。但是有时候所求是立体图形不在一个平面上的两点,那么怎么来求两点之间的最短距离呢?中公教育专家认为,此时就需要我们运用空间想象的能力,将立体图形展开成为平面图形进行求解。
1.方法:利用空间想象力,把立体图形展开成一个平面图形,利用最短或最远距离解题。
2.关键:在求解过程中,会涉及到最短或最远距离,要能找到这些距离。平时在生活中,可以多画一画立体图的展开图,培养自己的空间想象力。
1.有一个长方体如图所示,上下两个面是正方形,边长为a,高为2a,若从A点到B点的表面最短距离的连线与边CD相交与F点,已知BF长为10,求这个长方体的体积?
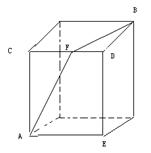
A.90 B.90 C.540 D.
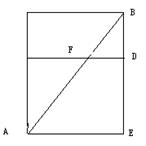
【中公解析】由题意可将A点和B点最短距离的连线划出,交CD于F点,得到图形如图,由相似三角形知道,BD:BE=BF:AB=1:3,所以知道AB连线为30,由三角形ABE勾股定理得到,
平面如图:
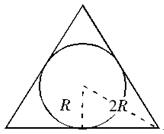
2.颗气象卫星与地心距离相等,并可同时覆盖全球地表,现假设地球半径为R,这3颗卫星距地球最短距离为()。
A. R B. R C.R D.2R
【中公解析】3颗卫星组成的平面与地球相切时距离最短且可覆盖全球表面。如图所示,等边三角形顶点到其内接圆圆心距离为2R,卫星距离地球最短距离为R。故选择C选项。
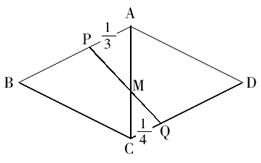
3.如图,正四面体ABCD,P、Q分别是棱AB、CD的三等分点和四等分点(AB=3AP=4CQ),棱AC上有一点M,要使M到P、Q距离之和最小,则MC∶MA=( )。
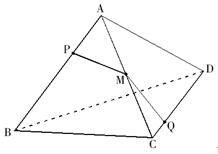
A.1∶2 B.4∶5 C.3∶4 D.5∶6
【中公解析】如图展开,PQ为最短距离。△APM与△CQM相似,MC∶MA=CQ∶AP=3∶4。故选择C选项
关注四川中公教育微信scoffcn,政策问题实时答,考试信息不漏看。
注:本站稿件未经许可不得转载,转载请保留出处及源文件地址。
设为首页 | 加入收藏 | 关于我们 | 联系方式 | 版权声明 | 招生代理 | 支付方式 | 网站地图 | 手机页面 | 友情链接
Copyright©1999-2018 北京中公教育科技股份有限公司 .All Rights Reserved京ICP备10218183号 京ICP证161188号 京公网安备11010802020593号 出版物经营许可证新出发京批字第直130052号
京公网安备11010802020593号 出版物经营许可证新出发京批字第直130052号