2018四川公务员考试行测技巧：如何判断排列组合中相加还是相乘

在行测考试中，排列组合问题最基础的就是两个基本计数原理，而许多同学往往分不清到底是将方法数相加还是相乘。所以，今天我们就加法原理和乘法原理的区别来和大家分享一下经验。

排列组合问题是研究在一定条件下完成一件事情方法数的计数问题。所以区分是用加法还是乘法只要去考虑这件事我们是分类完成的还是分步完成的即可，需要记住分类相加，分步相乘。以下面的两道例题为例：

【例1】某地有甲乙丙三个站台，从甲站到乙站有6种不同出行方式可以选择，从乙站到丙站5种不同出行方式可以选择，从甲站到丙站有4种不同出行方式可以选择，则甲站到丙站有( )种不同出行方式可以选择?

A.26 B.27 C.34 D.37

【答案】A

【解析】这道题既需要分类也需要分步。先分成两类情况，一类是从甲直达丙，有6种;另一类是从甲经过乙再到丙，这一类中涉及分步的问题，有5×4=20种。则完成从甲站到丙站这件事的方法数将两类情况数相加即可，一共有6+20=26种方法，选A。

【例2】给如图所示的4个区域涂上颜色，可得到一个漂亮的“太极图”，现有红、黑、黄、蓝4中颜料供选用，要求每个区域只能涂一种颜色，且相邻的区域颜色不同，则不同的涂色方法的种数为多少?

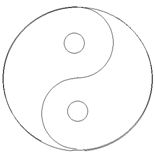
A.81 B.108 C.144 D.156

【答案】B

【解析】因为我们知道涂色没办法一次完成，需要各个区域依次去涂，所以这道题需要分步。则这四个区域依次有4种，3种，3种，3种选择。将每一步的方法数相乘，共有4×3×3×3=108种，选B。

相信同学们通过上面两道例题的学习，对两个计数原理已经有所了解，但要想实际在国考中更好的解决此类问题，还是需要同学在平时的学习过程中勤加练习。

注：本站稿件未经许可不得转载，转载请保留出处及源文件地址。